What is an Algorithm?

My understanding, its just mathematics. In its earliest form, its a set of equations derived to solve problems. In computer science, everyone talks about Algorithms and its use cases. Programming is a form of algorithm, because you create a code to solve a problem. So what is the use of an algorithm in computers, in essence algorithms used in computers help to compute our daily tasks from generating a word document to loading a webpage and displaying it on your screen.

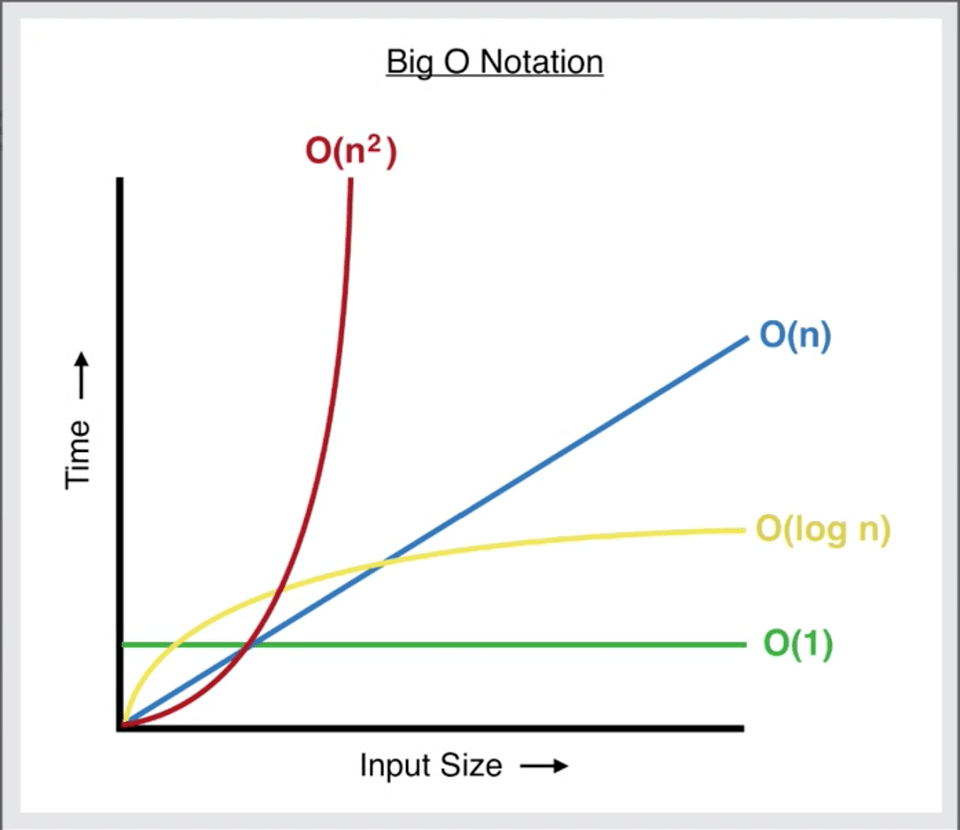
Algorithms are used in combination with data, to be more precise data structures. Data structures are your variables, arrays, lists, dictionary, complex data managed and/or organised that is efficently managed by an algorithm to access and modify the data. How we determine efficiency of an algorithm, is by determining the space and time complexity commonly understood as the big-o notation.

Basic O(n) - Linear Search

O(n) or O(1) is the simplest expression, or linear time. If 'n' is 1, the computer only executes 1 task, if 'n' is > 1. The computer executes 'n' number of tasks. Thus the time increases in a linearly upwards as more tasks is computed. Is this efficient? Yes and No.

• In its best case scenario, you can find the answer immediately. O(1)
• In its worst case, it will traverse through every single task to find your answer. O(n)

Imagine you have a dictionary and you want to search the word, starting with the letter "Z". However you turn it page by page, how long would you take to reach the letter "Z". Not so efficently now right?

Basic O(log n) - Binary Search

O(log n) or commonly known as divide and conquer. As its name goes, the computer executes the first task in the middle, if the value is more or less than the answer it discards the first half/second half. Then executes the second task in the middle of the new half.

Imagine you have a dictionary and you want to search for the word, starting with the letter "K". You open up midway of the dictionary to find that you are at "M". "M" is more than "K" in the sequence, you then discard the letters above "M" and start your search midway from "A" to "M". You open up midway to find that you are at letter "F", "F" is less than "K" in the sequence. So you discard the letters lesser than "F". And restart your search from "F" to "M", midways you reach "I" which is still less than "K" so you discard the letters less than "I" and restart your search to the middle of "I" to "M". You finally find "K".

• In its best case scenario, you can find the answer immediately. O(1)
• In its worst case, you will traverse halfways each point until you find your answer. O(log n)

Basic O(n2) - Bubble Sort

Well as you might know this is the worst case scenario for any search algorithm. It takes the longest time and it grows exponentially with 'n'. To simply put it is (n * n).

Imagine your dictionary is torn and you have to piece back each page 1 by 1 in its order "A" to "Z". You have to check each Letter by its priority and swap the pages from the 1st page to the nth page.

• In its best case scenario, you can find the answer Ω(n)
• In its worst case, you have to go through the entire n pages to sort it. O(n2)